2024年省考行测备考之利用“捆绑法”解决排列组合中的相邻

　　葫芦岛华图为您提供最新的备考文章：2024年省考行测备考之利用“捆绑法”解决排列组合中的相邻 更多招聘信息敬请关注 葫芦岛华图招聘频道(http://huludao.huatu.com)或关注 葫芦岛华图教育微信公众号(hldhuatujiaoyu),葫芦岛华图咨询电话：(0429-2133212)。

　　近几年的国考真题中，排列组合问题属于必考题型。在排列组合问题中，有时我们会看到题目中会有“相邻、连在一起、不能分开、挨着”等描述，当出现这类描述的时候我们就可以用今天要分享的“捆绑法”去解题。

　　题型标志：

　　题干中出现“必须相邻、必须相连、不能分开”等表述的排列组合问题

　　二、方法介绍：

　　(1)先将要求相邻的元素捆绑在一起作为一个整体与其它元素排列;

　　(2)再对捆绑在一起的元素内部进行排列

　　如：有红、橙、黄、绿、蓝、紫6种颜色的玩具小车各1辆，现将它们排成一列且要求绿色和蓝色的小车挨在一起，共有多少种排列方式?

　　A.48

　　B.240

　　C.480

　　D.720

　　题干要求“绿色、蓝色小车挨在一起，问排列方式”，考虑用“捆绑法”解题。

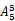
　　将蓝色与绿色的玩具车捆绑在一起当作1个整体与其它4辆玩具车排列，此时先让5个整体排列，有=120种排列方式，然后捆绑在一起的蓝绿色小车内部又有A22=2种排列方式，所以有120×2=240种排列方式，结合选项选B。

　　三、真题讲解：

　　【例1】某场科技论坛有5G、人工智能、区块链、大数据和云计算5个主题，每个主题有2位发言嘉宾。如果要求每个主题的嘉宾发言次序必须相邻，问共有多少种不同的发言次序?

　　A. 120

　　B. 240

　　C. 1200

　　D. 3840

　　【答案】D

　　【解析】本题考查排列组合问题，用捆绑法解题。

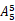
　　先把每个主题的2个人捆绑在一起，形成5个整体进行排列，有=120(种)排列方式，然后每个整体内部是2个人，5个整体的内部排列共有(A22)5=32种排列方式。故共有120×32 =3840(种)发言次序。

　　因此，选择D选项

　　【例2】为加强机关文化建设，某市直机关在系统内举办演讲比赛，3个部门分别派出3、2、4名选手参加比赛，要求每个部门的参赛选手比赛顺序必须相连，问不同参赛顺序的种数在以下哪个范围之内?

　　A. 小于1000

　　B. 1000-5000

　　C. 5001-20000

　　D. 大于20000

　　【答案】B

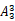
　　【解析】本题考查排列组合问题，用捆绑法解题。题目要求“每个部门的参赛选手比赛顺序必须相连”，利用捆绑法，先将每个部门视为一个整体，3个部门视为3个整体则参赛顺序有=6种，然后3个部门内部也需各自排序，依次为A33=6、A22=2 、A44=24 。

　　总共的排序有：A33×A33×A22×A44=6×6×2×24=1728(种)。

　　因此，选择B选项。

　　通过以上几道例题的练习，想必大家对“捆绑法”也有了一定的了解，在后续的备考过程中，通过多练习，一定能掌握此种方法!

　　【思维导图】

【省考课程】|【国考课程】|【事业单位课程】|【教师招聘课程】

【医疗招聘课程】|【金融招聘课程】|【公安招警课程】|【军队文职课程】